|
|

 IE-Modelは,Hortonの浸入能方程式と, IE-Modelは,Hortonの浸入能方程式と,
蒸発散サブモデルを組み込んだ集中定数型の長期間流出モデルである.
モデルの構造は右図に示す通りで,流域に降った降雨の一部は樹幹・樹冠により遮断される.
地上に到達した降雨の一部は不浸透域へ分配され,直接河川へと流出する.
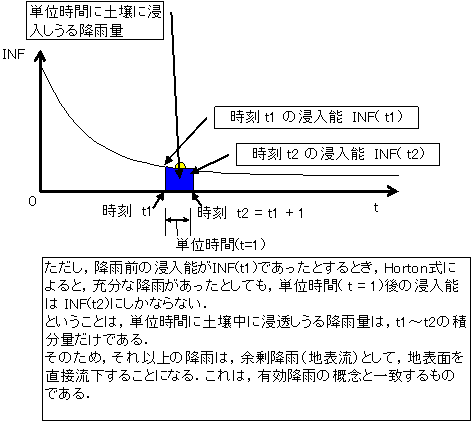
浸透域に降った降雨は,Horton型の浸入能方程式に従って決定される時々刻々の浸入能に従って土壌へと浸入する成分と,余剰降雨となって直接流出する成分とに分かれる.
土壌へと浸入した雨水が,圃場容水量に達するとさらに下層へと浸透を開始する.
降雨終了後,徐々に表層土壌が乾燥するに従って蒸発散量が減少する様を表現した蒸発散サブモデルにより,土壌水が蒸発し浸入能を回復させる.

Horton型の浸入能方程式を前提として雨水を土壌中へ浸入させる.

この浸入能方程式を積分すると,土壌水分量を表すことができる.
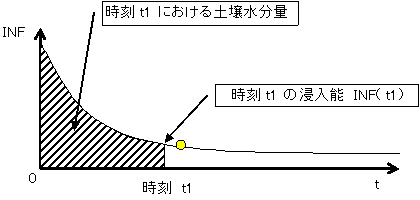
一般に,土壌中に充分な水分量が供給(浸入)されると,それまで毛管力などで土壌中に保持されていた水分量が,重力による作用に耐えきれなくなって,より下層へと流下(浸透)し始める.下層へと流下し始めるときを”圃場容水量”といい,pF1.8に相当する.
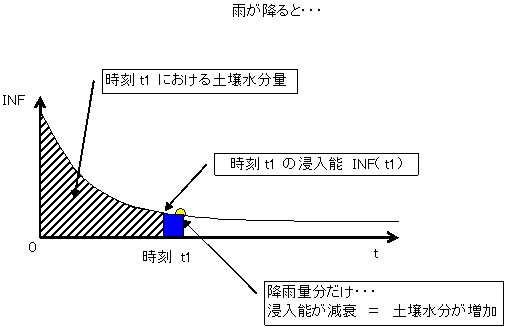
このモデルでは,この作用を考慮するため,圃場容水量に相当する土壌水分量になって始めて地下への浸透を開始するように考えられている.実際には,土地利用毎に圃場容水量時の浸入能 INFF18をあらかじめ求めておき,任意時刻の浸入能がINFF18より小さくなっていれば地下浸透量に相当する分だけ土壌水分量が減少するよう計算する.
なお,地下浸透量は,これまでの研究により土壌水分量に寄らずほぼ一定値であることがわかっており,その量は最終浸入能に一致することが示されているため,このモデルでもそのように扱っている.
降雨による浸入能の減衰と地表流の考え方.
蒸発による浸入能の回復
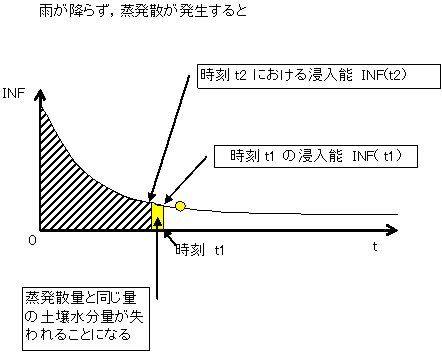

蒸発散は,浸入能の回復という現象で表される.この浸透域の蒸発散量は以下のように行う.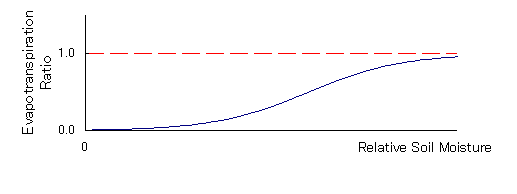
まず,時間t'における浸入能から,次式により土壌水分(SWt')を計算する.
SWt' = ∫ [ f∞ + ( f0 −f∞) exp(-αt ) ]dt (1)
これを飽和土壌水分量で割り土壌水分率(SW)を求め,(2)式に代入して,蒸発散比(ETR)を決定する.
PET
ETR = ―――――――――― (2)
1 + EA・exp( -EB・SW)
ここで,ETR;蒸発散比,PET;上限値,EA,EB;係数,SW;土壌水分率(飽和土壌水分量に対する土壌水分量)である.
(2)式は,流域の乾湿の影響を受ける蒸発散現象を表している.すなわち晴天が続くと流域は乾燥し,蒸発散に利用される水分が制限され,地域からの蒸発散量は減少する.このエネルギー余剰の大半が顕熱フラックスとして消費されるため大気の乾燥力が高まり,可能蒸発量は増加する.よって蒸発散比は小さくなる.
一方,降雨が続くと流域全体が湿潤となり,可能蒸発量と蒸発散量は近似的に近くなる.よって蒸発散比は1に近づく.実際の現象はこの間を滑らかに推移していると考えられ,蒸発散比と土壌水分はFig.に示すようなS字曲線を描くように(2)式が定義されている.
こうして土壌水分より決定された蒸発散比に可能蒸発量をかけた値が,求める蒸発散量(Et)となり,浸入能の回復に寄与する.
|
|

