MMD study

Part 6. MMD Know How - 回転補正

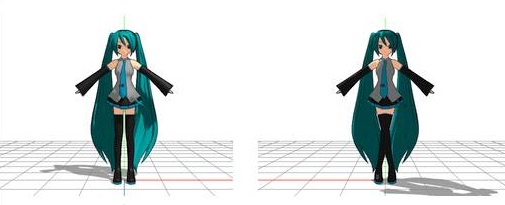
MMDの特性 MMDを使い始めると、MMDの雑誌には書かれていない現象に出食わすことがあります。 その中の一つに、「モデルを回転させると両足の位値がずれる」という問題があります。 例えば、 上図の左側は「正面の向き」の姿勢、右側は 180度回転して裏側から見た姿勢です。 左右の足が交差してますよね！ この交差をなくすように X軸方向に左右の足を微調整し動かして観察した結果、 　左足_IK(0, 0, 0) → 左足_IK(-1.5, 0, 0) 　右足_IK(0, 0, 0) → 右足_IK(+1.5, 0, 0) とすると元の「正面の向き」の姿勢と同じになることが分かりました。 さらに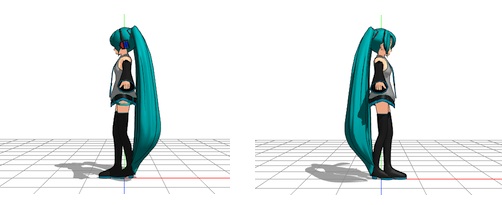 左図は「右向きに 90度回転」した姿勢、右図は「左向きに 90度回転」した姿勢です。 左右の足がずれてますよね！実際には、X軸方向かつZ軸方向にもずれてます。 このずれをなくすように X軸方向に左右の足を微調整し動かして観察した結果、 「右向きに 90度回転」した場合は、 　　左足_IK(0, 0, 0) → 左足_IK(0, 0, -0.75) 　　右足_IK(0, 0, 0) → 右足_IK(+1.5, 0, +0.75) 「左向きに 90度回転」した場合は、 　　左足_IK(0, 0, 0) → 左足_IK(-1.5, 0, +0.75) 　　右足_IK(0, 0, 0) → 右足_IK(0, 0, -0.75) とすると元の「正面の向き」の姿勢と同じになることが分かりました。 より深く調べると 実は、45度単位の回転で調べると、もっと複雑な状況になることが分かって来ました。 このような経験則をもとにして、回転補正の規則をまとめてみました。 回転補正 「ひっくり蛙の法則」 時計 ik_T(y) L_ik R_ik 0:00 0 L=(0, 0, 0) R=(0, 0, 0) 1:30 - 45 補正 L=*(0, 0, - γ) R=*(+β, 0, +γ) 3:00 - 90 補正 L=*(0, 0, - β) R=*(+α, 0, +β) 4:30 - 135 補正 L=*(- β, 0, - γ) R=*(+α, 0, +γ) 6:00 180 補正 L=*(- α, 0, 0) R=*(+α, 0, 0) 7:30 + 135 補正 L=*(- α, 0, +γ) R=*(+β, 0, - γ) 9:00 + 90 補正 L=*(- α, 0, +β) R=*(0, 0, - β) 10:30 + 45 補正 L=*(- β, 0, +γ) R=*(0, 0, - γ) 12:00 0 L=(0, 0, 0) R=(0, 0, 0) 補正値：　α= 1.5　β= 0.75　γ=0.38 この補正値が正確かどうかは保証できませんが、まあ大丈夫！ 黄色：ダンスで頻繁に出て来る角度。＊印：補正を忘れちゃダメ！(強調)。 coffee break 回転補正が必要な理由は分かりましたが、なぜMMDはこんな特性になっているの？ その根拠は？ちょっと想像してみます。 - 頭と両足の位値(x, z)を原点(0, 0)に置いて、180度反転すると位置は原点(0, 0)のまま。 これが単純な考えですが、足幅あるいは靴幅の実装を考えるとそう簡単ではなくなる。 - 普通に考えれば、頭は原点(0, 0)、靴幅の実装を想定して、左足(+0.75, 0)、右足(-0.75, 0)と初期設定しておけば、 ひっくりかえした時に、頭は原点(0, 0)、左足(-0.75, 0)、右足(+0.75, 0)となって対照的、これが分かり易いと思うのだが。 - MMDの創設者は、正面に立ったときに「両足を原点(0, 0)」としたかったのだと思います。 そのために、「左足のX軸」をあらかじめ X=-0.75 ずらし、「右足のX軸」をX=+0.75 ずらしておこうと考えたのではないか。 - 結果、正面では、頭(0, 0)、左足(0, 0)、右足(0, 0)となってシンプル、拍手！ その副作用が裏面に、頭(0, 0)、左足(+1.5, 0)、右足(-1.5, 0)となるなど、全体が非対称でややこしくなっている . . . 泣き！ - MMDモデルたちの姿を観察すると、足幅や靴幅の大小の差など個性があって、 原点に立ったときの足の格好が若干違った風に見えなくもない。これは「左右足のX軸」が一律に0.75ずれていると認識すれば、なるほどガッテン！

Top page of Linedance Animation