 |
|
このページの最後へ
少し前ですが、ふとNHK3chのTVを見ていたらこんな話をしてました。 小学生向けの番組「トゥトゥ」というリコーダの教室ですが、 「今日は笛の作り方を教えましょう」 「わらや、ストローをこんな風に切って作ればいいんです」
これを長さを3分の2にカットすると、ソ音ができます
ソ音 
これを長さを3分の2にカットすると、レ音ができます
レ音 
この長さを2倍にすれば、ほら低いレ音ができるでしょう
レ音 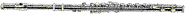
同様にして、レ音からラ音、そしてラ音からミ音が作れます。 これを繰り返せば、ド、レ、ミ、ファ、ソ、ラ、シ、ド、の音階の笛ができあがり。 これを発見したのは、古代ギリシャの哲学者パスカルという人なんですよ。 確か、こんなストーリだったと記憶しています。 なるほど、しかしこんな高級な理論を小学生が理解できるかなと思ったわけ。
音楽の理論の本、「学典」を開くとどの本でも最初にピタゴラスの話があります。 ランダムハウスの辞書で 引くと、 "Pythagoras" ピタゴラス、紀元前582年〜500年、ギリシャの哲学者、数学者、宗教家 "Pythagorean sacle" ピタゴラス音階、完全5度を積み重ねた音列から導き出された音階。 ピタゴラス学派の数学理論から生まれた。 "Pythagorean theorem" 幾何、ピタゴラスの定理。 さて、「学典」では ドレミファソラシドの音からなる音楽は古くはギリシャ時代にさかのぼる。 そのころすでに、振動数が1:2の関係にある2つの音は、同時に鳴った時は ほとんど1音のように響くことが知れていた。 ギリシャの数学者ピタゴラスは、さらに、振動数が2:3の関係にある2つの音が 完全5度(Perfect 5th)の関係にあり、良い音に響くことを発見した。 これはピタゴラスの黄金分割とも言われる。
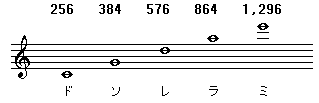
これはド音=256Hzとした時に、振動数が2:3の完全5度の関係にある音を 計算して求めたものです。 「ド、ソ、レ、ラ、ミ、おや? この5音はペンタトニックの構成音ですね」 と気がつく人はさすが。ペンタトニックはこちら さて、ピタゴラス音階、つまり完全5度を積み重ねた音列から導き出された音階を 計算して完成させて見ました。

(注意:振動数の値は、スペースの関係で、小数点第2位以下を切り捨て) これで一応は完成なのですが、 C音=256Hzのオクターブ上が、C音=512Hzのはずでなのに、 ピタゴラス音階では、B#音=518.9853Hzとり、B#音がC音と一致しない。
再び、「学典」を開くと、最初のピタゴラスの話の次にアルキタスという人物 が登場します。ランダムハウスの辞書には載っていませんが。 "Archytas" アルキタス(紀元前430年〜360年)は、長3度を構成する2音の 振動数を4:5にすると美しい響きが得られることを発見した。 これを純正長3度という。 これはド音=256Hzとした時に、ミ音=320Hzということです。 なお、ピタゴラス音階では、ミ音=324Hzであってずれていました。 ピタゴラスの完全5度(P5)と、アルキタスの純正長3度(M3)と の原理を元にして、純正律(Pure Temperament)の音律が作られた。

この図から分かるように、Triad(3つの音からなる和音)が良い響き となるように作られているのが味噌ですね。
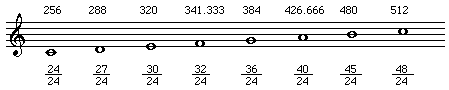
「学典」を読むと、 純正律は、アンサンブルをする上での必要性から生まれた発想である。 この音律に基づいて楽器を調律して演奏すると非常に美しい響きが得られる。 しかし次の欠点がある。 (1)ピアノなど鍵盤楽器では、一度Tuningしたら、転調が不可能となる。 (2)ド音とレ音との振動比は、8:9 であるが、レ音とミ音は、9:10である。 つまり同じ全音の中にも、大全音と小全音があることになる。 上記の意味を解釈すると、 「作曲家がイメージした調に従って」楽器を調律して演奏する、つまり 管楽器や弦楽器の演奏者は吹き方や指使いで微妙に音程を変える必要がある。 例えば、フルートのアンサンブルなんかもそういうことが必要らしい。
純正律の欠点をクリアするために考えられたものが平均律。 「学典」では、 平均律とは、オクターブを数学的に12等分したもので、物理的に得られる ものではないから、純正律に比べればいくらか響きがにごったりするが、 合理的で転調もうまくできるし実に便利なものであった。 そこで、だいたいバッハの時代あたりから以降のヨーロッパ音楽は、 この平均律による調性がおおもととしてあって、それが大発展した。 数学的に12等分という意味は、オクターブを12個の半音に分割し、 その半音の差のある2つの音の振動比を全て統一にすること。 電卓でその値を求めると、「2の12乗根」=1.059463094 これを使って、平均律での振動数を計算しておきます。 比較のために純正律などの値も書いておきます。これを眺めると、アンサンブルなどをする場合において、 純正律に近づけるためにはどの音を微妙に↑↓する必要があるか、 という理屈だけは分ったような気がしませんか。
"Pythagorean sacle" 、ピタゴラス音階は 「完全5度(Perfect 5th)」を積み重ねた音列から導き出された音階。 F→C→G→D→A→E→B→F#→C#→G#→D#→A#→E#→F これを全く逆さまに進行すると、 つまり「完全5度下がる」あるいは「完全4度上がる」わけですが、 F←C←G←D←A←E←B←F←C#←G#←D#←A#←E#←F これは、Jazzのコード進行の基本中の基本である「Cycle of 5th」 と呼ばれている循環コードです。 Jazzでは「シャープ」よりも「フラット」をよく使うので 置き換えて並びを整えると、 B→E→A→D→G→C→F→Bb→Eb→Ab→Db→Gb→Bそれでは、典型的なブルース形式の曲を一つの例にとって、 「Cycle of 5th」のJazz風味を確かめて下さい!こちらです。
 Be-BopスタイルのBlues
Be-BopスタイルのBlues
 coffee break
coffee break
ピタゴラスの定理を解説するデモ、Javaのアプレットで作ってみました。うそ!
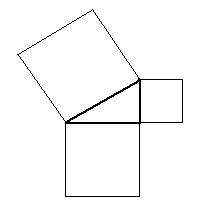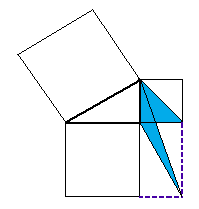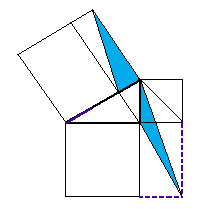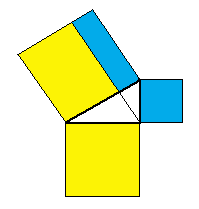 ここ
ここ
もし動かなければ「ここ」をクリックしてみて下さい。 実は、以前に、JavaのJDKか何かのサンプルプログラムの中に、 こんな例題があったのを思い出して、アニメgifで作ったものです。 話は脱線しますが、 このアニメgifは、小学校あるいは中学校の授業で、 生徒に自由な発想で作らせて遊ばせるツールとして適当な気がします。 笑い話し 「ただしいこたえのばんごうをマルでかこみなさい」 という問題に、その幼い子は、 正解の数字の周囲を小さな丸をいくつもつなげて一心に囲んでいた。 「ダメよそんなの。こうやるのよ」と教えていたら、 その子の発想力は育つであろうか。